Page 157 - 《社会》2013年第1期

社会· ２０１３ · １

析加以证实，这是一个统计分析的问题，本文的第四部分将再予以分析。
（三）数学模型
本文采用的统计模型为结构方程模型 ５ ，目的是通过其中的测量
模型建立起观测变量与潜变量之间的关系，使潜变量具有可靠的测量
基础，以此解决抽象概念的操作化问题，进而通过结构模型分析潜变量
之间的关系。结构方程模型的一般表达式可写为：
狔 ＝Λ 狔 η ＋ ε （ １ ）
狓 ＝Λ 狓 ξ ＋δ （ ２ ）
（ ３ ）
η ＝Β η ＋Γ ξ ＋ ζ
狔
其中， 狓 为外源观测变量， 为内生观测变量， ξ 指外源潜变量， η
指内生潜变量； ε 、 δ 和 ζ 则为三个模型的误差项或残值。（ １ ）式和（ ２ ）
式为测量模型，反映的是观测变量和潜变量之间的关系，实质是验证性
因子分析。（ ３ ）式为结构模型，反映的是外源潜变量和内生潜变量之间
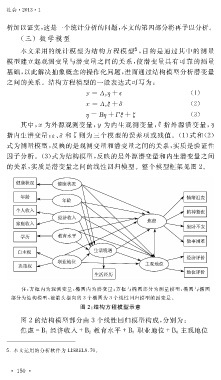
的关系，实质是潜变量之间的线性回归模型。整个模型框架见图 ２ 。

注：方框内为观测变量，椭圆内为潜变量；方框与椭圆部分为测量模型，椭圆与椭圆
部分为结构模型，被箭头指向的 ３ 个椭圆为 ３ 个线性回归模型的因变量。
图 ２ ：结构方程模型示意

图 ２ 的结构模型部分由 ３ 个线性回归模型构成，分别为：
主观地位
焦虑 ＝犅 １ 经济收入 ＋犅 ２ 教育水平 ＋犅 ３ 职业地位 ＋犅 ４

５． 本文运用的分析软件为 犔犐犛犚犈犔８．７０ 。

· １ ５ ０ ·