Page 126 - 《社会》2018年第3期

性别视角下的“农转非”路径及其收入回报

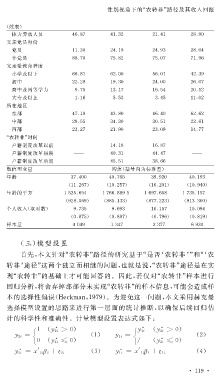
（续表）
体力劳动人员 ４６．８７ ４１．３２ ２１．４１ ２８．９０
父亲党员身份
党员 １１．３０ ２４．１８ ２４．９３ ２８．０４
非党员 ８８．７０ ７５．８２ ７５．０７ ７１．９６
父亲受教育程度
小学及以下 ６６．８１ ６２．００ ５６．０１ ４２．３９
初中 ２２．２８ １９．３０ ２４．００ ２６．０７
高中及同等学力 ９．７５ １３．１７ １６．５４ ２０．５２
大专及以上 １．１６ ５．５３ ３．４５ １１．０２
所在地区
东部 ４７．１８ ４３．８０ ４６．４０ ６２．６２
中部 ２９．５５ ３４．３０ ３０．５１ ２２．６１
西部 ２３．２７ ２１．９０ ２３．０９ １４．７７
“农转非”时间
户籍制度改革以前 ——— １４．１８ １６．８７ ———
户籍制度改革初期 ——— ４０．３１ ４４．４７ ———
户籍制度改革后期 ——— ４５．５１ ３８．６６ ———
数值型变量 均值（括号内为标准差）
年龄 ３７．４００ ４０．７６５ ３９．９２０ ４０．１９３
（ １１．２６７ ） （ １０．２５７ ） （ １０．２０１ ） （ １０．９４０ ）
年龄的平方 １５２５．６５４ １７６６．８８９５ １６９７．６５８ １７３５．１５７
（ ９２８．０６９ ） （ ８８５．１３３ ） （ ８７７．２２３ ） （ ９１３．３００ ）
个人收入（取对数） ９．７３５ ９．６９３ １０．１５７ １０．０９４
（ ０．８７５ ） （ ０．８８７ ） （ ０．７９６ ） （ ０．８１９ ）
样本量 ４０４９ １３４７ ２３７７ ６９３０

（三）模型设置
首先，本文针对“农转非”路径的研究基于“是否‘农转非’”和“‘农
转非’途径”这两个独立而相继的问题，也就是说，“农转非”途径是在实
现“农转非”的基础上才可能回答的。因此，若仅对“农转非”样本进行
回归分析，将舍弃掉那部分未实现“农转非”的样本信息，可能会造成样
本的选择性偏误（ 犎犲犮犽犿犪狀 ， １９７９ ）。为避免这一问题，本文采用赫克曼
选择模型设置的思路来进行第一层面的统计推断，以确保后续回归估
计的科学性和准确性。计量模型设置表达式如下：
狔 ２犻 ＞０ ）
狔 ２犻 ＞０ ）

１ （  狔 １犻 （ 
烄 烄
狔 ２犻 ＝ 烅  （ １ ） 狔 １犻 ＝ 烅  （ ２ ）
／ （
０ （
烆 狔 ２犻 ≤０ ） 烆 狔 ２犻 ≤０ ）
狔 ２犻 ＝狓′ ２犻 β ２ ＋ ε ２犻 （ ３ ） 狔 １犻 ＝狓′ １犻 β １ ＋ ε １犻 （ ４ ）


· １ １ ９ ·