Page 206 - 《社会》2017年第1期

统计模型的“不确定性”问题与倾向值方法

型形式的不确定性。通过“贝叶斯模型平均法”和“奥卡姆窗口”原则，
我们得到 １２ 个 候 选 模 型。在 这 些 模 型 中，按 照 贝 叶 斯 因 子 （ 犅犪 狔 犲狊
犉犪犮狋狅狉 ）的数值排序，最后留下排在前五位的模型。 １０ 这些模型的累计
后验概率达到了 ７８％ ，说明通过这 ５ 个模型基本能够涵盖大部分的数
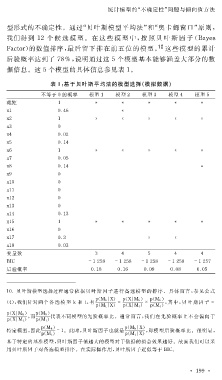
据信息。这 ５ 个模型的具体信息参见表 １ 。
表 １ ：基于贝叶斯平均法的模型选择（模拟数据）
不等于 ０ 的概率 模型 １ 模型 ２ 模型 ３ 模型 ４ 模型 ５
截距 １     
狓１ ０．４６ 
狓２ １     
狓３ ０
狓４ ０．０２
狓５ ０．１４
狓６ １     
狓７ ０．０５
狓８ ０．１４ 
狓９ ０
狓１０ ０
狓１１ ０
狓１２ ０
狓１３ ０
狓１４ ０．１３
狓１５ １     
狓１６ ０
狓１７ ０．３  
狓１８ ０．０３
变量数 ３ ４ ５ ４ ４
犅犐犆 －１２５８ －１２５８ －１２５８ －１２５８ －１２５７
后验概率 ０．１８ ０．１６ ０．０９ ０．０８ ０．０５

１０． 贝叶斯模型选择过程通常依据贝叶斯因子进行备选模型的排序。具体而言，参见公式
狆 （ 犕 犽 ｜ 犡 ） 狆 （ 犡 ｜ 犕 犽 ） 狆 （ 犕 犽 ）
（ ４ ），我们针对两个 备 选 模 型 犽 和 狋 ，有 ＝ × ， 其 中，贝 叶 斯 因 子 ＝
狆 （ 犕 狋 ｜ 犡 ） 狆 （ 犡 ｜ 犕 狋 ） 狆 （ 犕 狋 ）
狆 （ 犡 ｜ 犕 犽 ） ， 而 狆 （ 犕 犽 ） 代表不同模型的先验概率比。通常而言，我们在先验概率上不会偏向于
狆 （ 犡 ｜ 犕 狋 ） 狆 （ 犕 狋 ）
狆 （ 犕 犽 ） 狆 （ 犕 犽 ｜ 犡 ）
特定模型，因此 ＝１ 。此时，贝叶斯因子也就是 ， 即模型后验概率比。很明显，
狆 （ 犕 狋 ） 狆 （ 犕 狋 ｜ 犡 ）
基于特定的基准模型，贝叶斯因子值越大的模型对于数据的拟合效果越好。故而我们可以采
用贝叶斯因子对备选模型排序。在实际操作用，贝叶斯因子近似等于 犅犐犆 。

· １ ９ ９ ·