Page 208 - 《社会》2017年第1期

统计模型的“不确定性”问题与倾向值方法

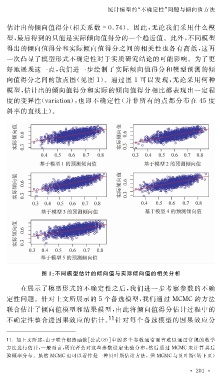
估计出的倾向值得分（相关系数 ＝０．７４ ）。因此，无论我们采用什么模
型，最后得到的只能是实际倾向值得分的一个趋近值。此外，不同模型
得出的倾向值得分和实际倾向值得分之间的相关性也各有高低，这再
一次凸显了模型形式不确定性对于实质研究结论的可能影响。为了更
好地展现这一点，我们进一步绘制了实际倾向值得分和模型预测的倾
向值得分之间的散点图（见图 １ ）。通过图 １ 可以发现，无论采用何种
模型，估计出的倾向值得分和实际的倾向值得分相比都表现出一定程
度的变异性（ 狏犪狉犻犪狋犻狅狀 ），也即不确定性（并非所有的点都分布在 ４５ 度
斜率的直线上）。

图 １ ：不同模型估计的倾向值与实际倾向值的相关分析

在展示了模型形式的不确定性之后，我们进一步考察参数的不确
定性问题。针对上文所展示的 ５ 个备选模型，我们通过 犕犆犕犆 的方法
联合估计了倾向值模型和结果模型，由此将倾向值得分估计过程中的
不确定性整合进因果效应的估计。 １１ 针对每个备选模型的因果效应分

１１． 如上文所述，由于联合似然函数［公式（ ８ ）］中的多个参数通常而言难以通过常规的数学
方法进行估计，一般而言，研究者会对这些参数设定先验分布，然后通过 犕犆犕犆 来计算其后
验概率分布。虽然 犕犆犕犆 也可以看作是一种贝叶斯估计方法，但 犕犆犕犆 与贝叶斯（转下页）

· ２ ０ １ ·