Page 212 - 《社会》2017年第1期

统计模型的“不确定性”问题与倾向值方法

（其变动范围如虚线所示）。这在一定程度上说明，这两种模型的估算
所得到的倾向值具有一定程度的差异性。
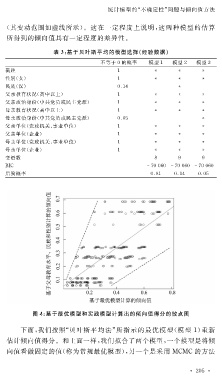
表 ３ ：基于贝叶斯平均的模型选择（经验数据）
不等于 ０ 的概率 模型 １ 模型 ２ 模型 ３
截距 １   
性别（女） １   
民族（汉） ０．１４ 
父亲教育状况（高中以上） １   
父亲政治身份（中共党员或民主党派） １   
母亲教育状况（高中以上） １   
母亲政治身份（中共党员或民主党派） ０．０５ 
父亲单位（党政机关、事业单位） １   
父亲单位（企业） １   
母亲单位（党政机关、事业单位） １   
母亲单位（企业） １   
变量数 ８ ９ ９
犅犐犆 －７００６０ －７００６０ －７００６０
后验概率 ０．８１ ０．１４ ０．０５

图 ４ ：基于最优模型和实践模型计算出的倾向值得分的散点图

下面，我们按照“贝叶斯平均法”所指示的最优模型（模型 １ ）重新
估计倾向值得分。和上面一样，我们拟合了两个模型，一个模型是将倾
向值看做固定的值（称为常规最优模型），另一个是采用 犕犆犕犆 的方法

· ２ ０ ５ ·