Page 245 - 《社会》2014年第5期

社会· ２０１４ · ５

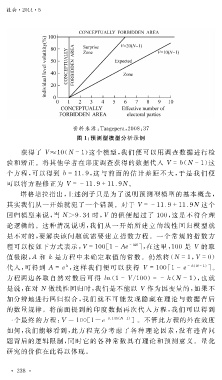
资料来源： 犜犪犪 犵 犲 狆 犲狉犪 ， ２００８ ： ３７
图 １ ：预测型模型分析示例
获得了 犞≈ １０ （ 犖－１ ）这个模型，我们便可以用调查数据进行检
验和矫正。将其他学者在印度调查获得的数据代入 犞＝犫 （ 犖－１ ）这
个方程，可以得到 犫＝１１．９ ，这与 前面 的估 计差 距不 大，于 是 我 们 便
可以将方程修正为 犞＝－１１．９＋１１．９犖 。
塔格培拉指出，上述例子只是为了说明预测型模型的基本概念，
其实我们从一开始就犯了一个错误。对于 犞＝－１１．９＋１１．９犖 这个
回归模型来说，当 犖＞ ９．３４ 时， 犞 的值便超过了 １００ ，这是不符合理
论逻辑的。这种情况 说 明，我 们 从一 开始 所建立 的线 性回归 模 型就
是不对的，要解决该 问 题 就需 要建 立指数 方程。一 个 常规的 指数方
程可以按如下方式表示： 犞＝１００ ［ １－犃犲 －犽犖 ］，在这里， １００ 是 犞 的取
值极限， 犃 和 犽 是方程中未确定取值的常数。仍然将（ 犖＝１ ， 犞＝０ ）
犽
代入，可得到 犃＝犲 ，这 样 我 们 便 可 以 获 得 犞＝１００ ［ １－犲 －犽 （ 犖－１ ） ］。
方程两边各取 自 然 对 数 后 可 得 犾狀 （ １－犞 ／ １００ ） ＝ －犽 （ 犖－１ ），也 就
是说，在对 犖 做线性回归时，我们是不能以 犞 作为因变量的，如果不
加分辨地进行回归拟 合，我们 就 不可 能发 现隐藏 在理 论与数 据 背后
的数量规律。将前面 提 到 的 印度 数据 再次代 入方 程，我们可 以得到
一个最终的方程： 犞 ＝１００ ［ １－ 犲 － ０．１４５ （ 犖－ １ ） ］。不管此方程的外在效度
如何，我们能够看到，此 方 程 充分 考虑 了各种 理论 因素，没有 违背问
题背后的逻辑限制，同 时 它 的 各种 常数具 有理 论和 预 测意义。量化
研究的价值在此得以体现。

· ２ ３ ８ ·