Page 123 - 《社会》2014年第5期

社会· ２０１４ · ５

险函数中，所以该模 型 不 估 计 常 数 项；第 二， 犆狅狓 模 型 的 基 准 风 险 函
数不可直接估计，但生存函数和累积风险率函数可以从模型中得到。
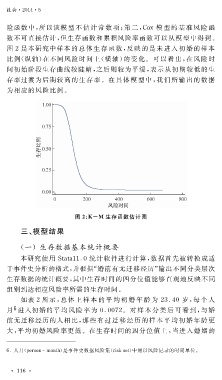
图 ２ 是本研究中样本 的 总体 生存 函 数，反 映的 是未进 入初婚 的样本
比例（纵轴）在不同风险时间上（横 轴）的变 化。可 以看 出，在 风险时
间初始阶段生存曲线较陡峭，之后则较为平缓，表示从初期较低的生
存率过渡为后期较 高 的 生 存率。在具 体模 型中，我 们 所输出 的数据
为相应的风险比例。

图 ２ ： 犓－犕 生存函数估计图

三、模型结果

（一）生存数据基本统计概要
本研究使用 犛狋犪狋犪１１．０ 统计软件进行计算，数据首先被转换成适
于事件史分析的格式，并根据“婚前有无迁移经历”输出不同分类层次
生存数据的统计概要，其中生存时间的四分位值能够直观地反映不同
组别到达相应风险率所需的生存时间。
如表 ２ 所示，总 体 上 样 本 的 平 均 初 婚 年 龄 为 ２３．４０ 岁，每 个 人
月 ６ 进入初婚的平 均 风 险 率 为 ０．００７２ 。对 样 本 分 类 后 可 看 到，与 婚
前无迁移经历的人相 比，那些 有 过迁 移经 历的样 本平 均初婚 年 龄更
大，平均初婚风险率更低。在生存时间的四分位值上，当进入婚姻的

６． 人月（ 狆 犲狉狊狅狀－犿狅狀狋犺 ）是事件史数据风险集（ 狉犻狊犽狊犲狋 ）中用以风险记录的时间单位。

· １ １ ６ ·